Array basic

What is Array?

An array is a collection of the same type of data stored in a contiguous memory space.

Note:

• Array’s subscripts start at 0.
• The array’s memory space is contiguous.

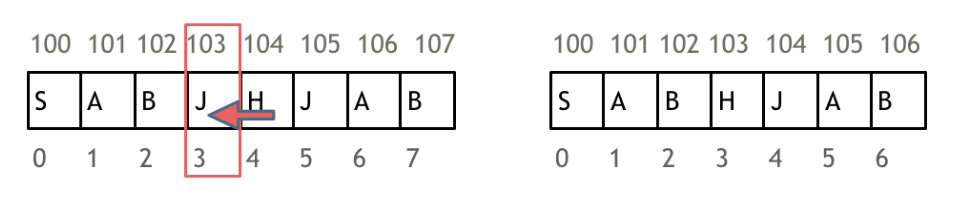
Since the array’s memory space is contiguous, we have to move other factors when we need to add or delete some factor in the array.

For example, when we need to delete an element with a subscript of 3, we inevitably need to move the following factors.

The array’s elements cannot be deleted; they are only overwritten.

Two-dimensional array memory space arrangement problem

In C++

void test() {
  int array[2][3] = {
    {0,1,2},
    {3,4,5}
  };
   cout << &array[0][0] << " " << &array[0][1] << " " << &array[0][2] << endl;
   cout << &array[1][0] << " " << &array[1][1] << " " << &array[1][2] << endl;
}

int main() {
  test();
}

The output is:

0x7ffee4065820 0x7ffee4065824 0x7ffee4065828
0x7ffee406582c 0x7ffee4065830 0x7ffee4065834

Note that the address is hexadecimal, so in C++, the two-dimensional array memory space is a continuous line.

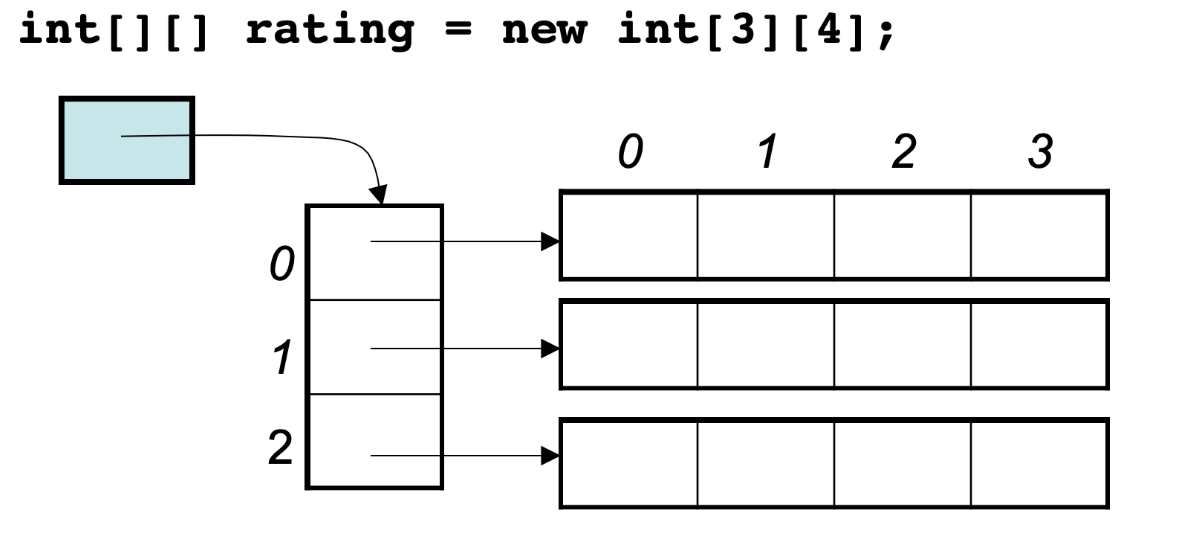
In Java

public static void test_arr() {
    int[][] arr = {{1, 2, 3}, {3, 4, 5}, {6, 7, 8}, {9,9,9}};
    System.out.println(arr[0]);
    System.out.println(arr[1]);
    System.out.println(arr[2]);
    System.out.println(arr[3]);
}

The output is:

[I@7852e922
[I@4e25154f
[I@70dea4e
[I@5c647e05

here is not a continuous number, so actually in Java the two-dimensional array memory space is like the following:

Binary Search

this problem’s prerequisites are:

• There are no duplicate elements in the array.
• The array is sorted.

You can’t solve this problem because you don’t understand the definition of interval.

Two methods of binary search： regarding right to left interval

The first method

Define the target in a left-closed and right-closed interval， which means[left, right]

The intervals definition decides how we write the code：

• While(left<=right) need to use <=，Since left==right meaningful，so we use <=
• If (nuts[middle]>target), then the right needs to be defined as middle-1, since currently, the middle’s location is not equal to the target， the next position to look for is the end subscript of the right-left interval, which is middle-1.

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1; // define target in [left, right] interval
        while (left <= right) { 
            int middle = left + ((right - left) / 2);// equal to (left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target in left interval，so [left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target in right interval, so [middle + 1, right]
            } else { // nums[middle] == target
                return middle; 
            }
        }
        // don't find the target
        return -1;
    }
};

• Time complexity：O(log n)
• Space complexity：O(1)

The second method

If the target is in a left-close and right-open interval， means [left, right)

• While(left<right) , use<, since left==right has no meaning in [left, right)
• If (nuts[middle]>target), since the current nuts[middle] is not equal to the target, continue searching in the left interval. The left interval is a left-closed, right-open interval, so update right to middle, because the next search interval will not compare the value of the right endpoint.

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size(); // define target in [left, right)
        while (left < right) { // Because when `left` equals `right`, the interval `[left, right)` is an invalid space, so use `<`.
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target in [left, middle)
            } else if (nums[middle] < target) {
                left = middle + 1; // target in [middle + 1, right)
            } else { // nums[middle] == target
                return middle; 
            }
        }
        return -1;
    }
};

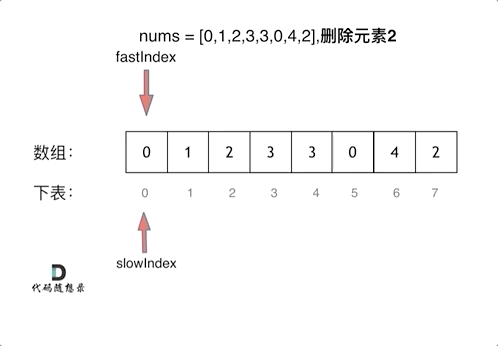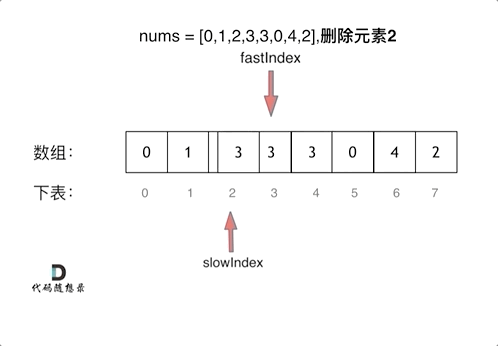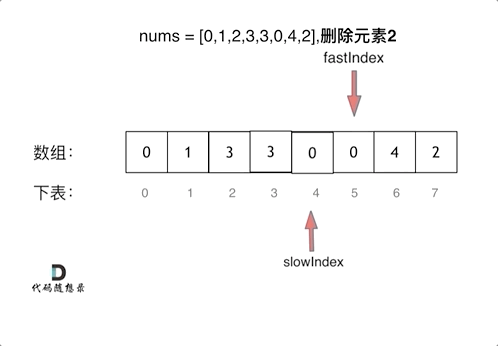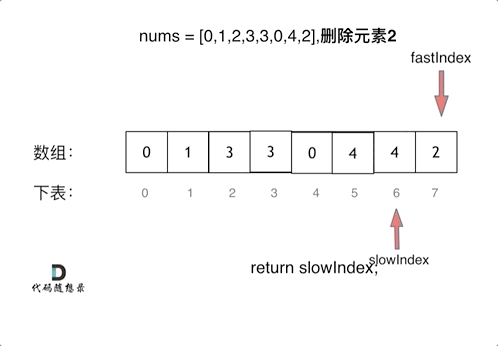
Remove element

The force solution uses the two-for-loop method.

The better solution is to use Fast-slow Pointers.

class Solution {
    public int removeElement(int[] nums, int val) {
        int left = 0;
        int right = nums.length-1;
        while(left<=right){
            if(nums[left]!=val){
                left++;
            }else{
                if(nums[right]==val){
                    right--;
                }else{
                    //replace
                    nums[left]=nums[right];
                    left++;
                    right--;
                }
            }
        }
        return left;
    }
}