Hashmap basic

What is HashTable

Official definition: A hash table is a data structure that allows direct access based on the value of the key.

To put it simply, an array is actually a hash table. In a hash table, the key is the index of the array, and you access the elements in the array directly through the index.

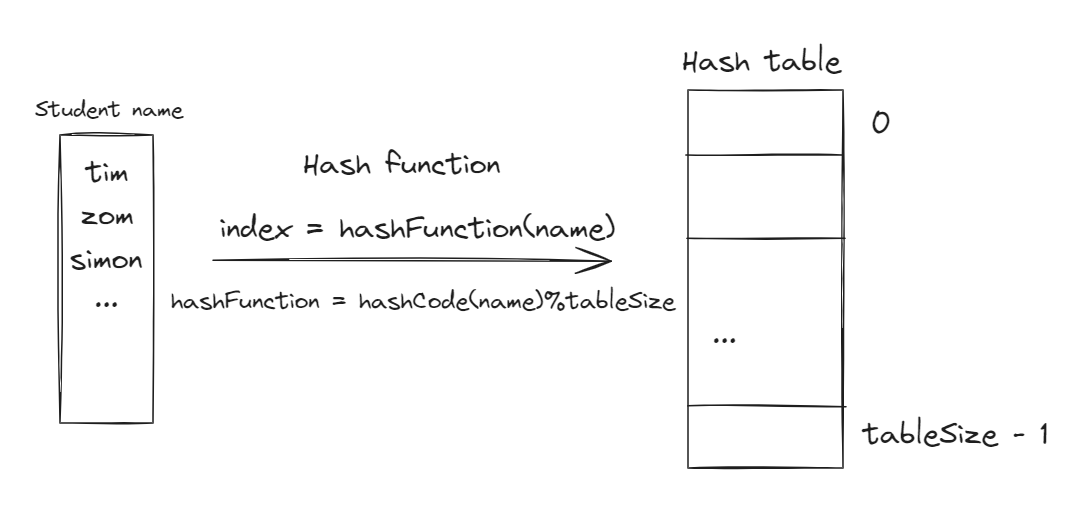
See the following picture:

So, what problem can a hash table solve? Generally, hash tables are used to determine whether an element appears in a set quickly.

For example, to check if a name is in a school’s records. Enumerating would have a time complexity of O(n), but using a hash table, it can be done in O(1).

We just need to initialise the hash table by storing all the students’ names from the school, and then during a query, we can directly know whether a student is in the school through the index.

Mapping student names to the hash table involves a hash function.

Hash function

Using the above example, we put the student’s name to an index in the hash table, you can quickly determine whether the student is in the school by querying the index.

What if the value obtained from hashCode is greater than the size of the hash table?

In this case, we perform a modulo operation on the value to ensure that the mapped index values fall within the hash table.

What if the number of students exceeds the size of the hash table?

Even if the hash function distributes the values evenly, it cannot prevent some student’s names from being mapped to the same index in the hash table.

So, we need to know hash collisions.

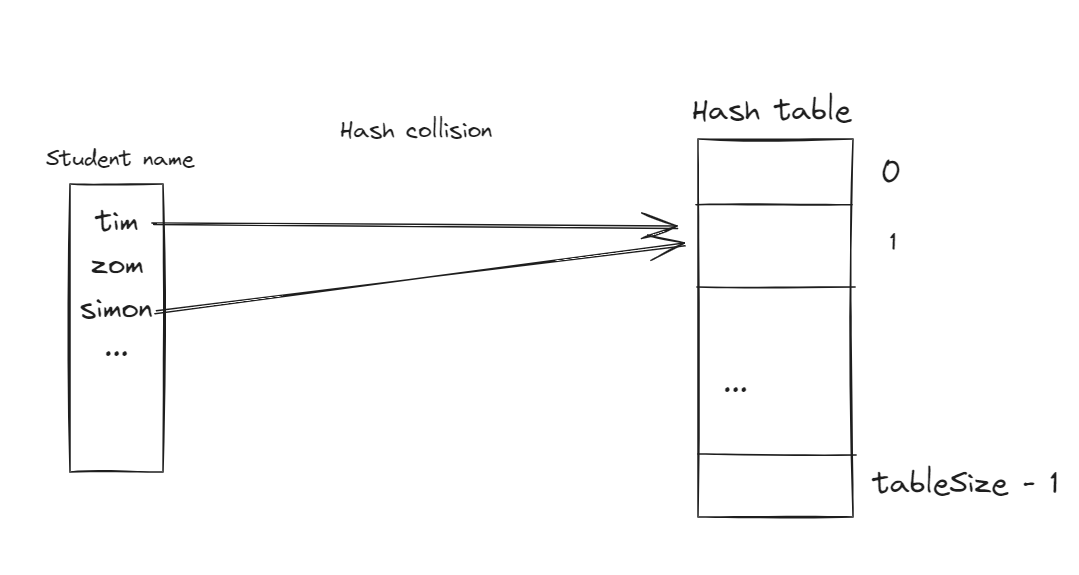
Hash collisions

In the following image, the tim and simon both mapped at the index of 1, this situation, we called “hash collisions.”

Solve hash collisions

Generally, there are two methods to resolve hash collisions: chaining and linear probing.

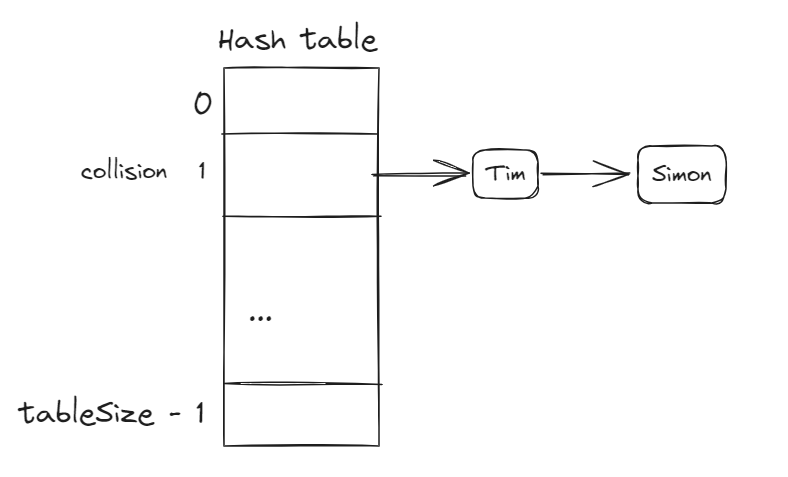
Method 1: Chaining

In the above example, Tim and Simon are both stored in index 1. We can use a linked list to store all the colliding elements, this way ,we can find both Tim and Simon through the index.

In fact, chaining requires choosing an appropriate size for the hash table so that it neither wastes a lot of memory due to empty array elements nor wastes too much time searching due to excessively long linked lists.

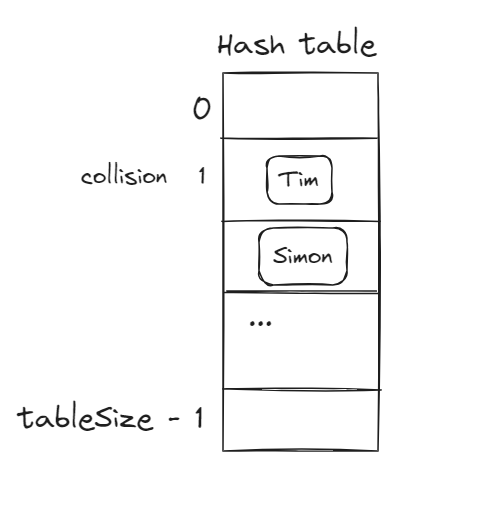
Method 2: Linear Probing

When using the linear probing method, you must ensure that the table size is greater than the data size. We need to rely on empty slots in the hash table to resolve collisions.

For example, if there is a collision at a position where Tim is placed, we then look for the next available slot to place Simon’s information.

Therefore, the table size must be greater than the data size; otherwise, there will be no empty slots in the hash table to store the colliding data.

Summary

To summarise, when we need to quickly determine whether an element appears in a set or other box, we should consider using the hash table

However, hashing trades space for time, as we need to use additional arrays, sets, or maps to store the data in order to achieve fast lookups.

Valid Anagram

Given two strings s and t, return true if t is an anagram of s, and false otherwise.

An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.

Example:

Input: s = "anagram", t = "nagaram"
Output: true

An array is a simple hash table; in this problem, the string only contains lowercase characters, so we can define an array to record the frequency of characters in string s.

How big of an array do we need? We can define an array called record with a size of 26, initialised to 0.

For example, given s = “aee”, t = “eae”;

Define an array called record to keep track of the frequency of characters in string s.

We need to map characters to array indices, which are essentially hash table indices. Since the ASCII values for characters ‘a’ to ‘z’ are 26 consecutive numbers, character ‘a’ maps to index 0, and correspondingly, character ‘z’ maps to index 25.

When traversing string s, we only need to perform an add one operation on the element at s[i] minus corresponding characters without remembering the ASCII value of characters. We just need to calculate a relative value.

Then, when traversing string t, we perform a minus one operation on the array index value mapped to each character in t.

Finally, we check if any element in the record array is not zero. If so, it means either string s or t has extra or missing characters, if so, we return false.

If all elements in the record array are zero, it means strings s and t are anagrams, so we return true.

class Solution {
    public boolean isAnagram(String s, String t) {
        int[] characters = new int[26];
      //Note: here we can't use Integer[] Since the original value of Integer[] is null.
        for (char c : s.toCharArray()) {
            characters[c-'a'] = characters[c-'a']+1;
        }
        for (char c : t.toCharArray()) {
            characters[c-'a'] = characters[c-'a']-1;
        }
        for (Integer character : characters) {
            if (character!=0){
                return false;
            }
        }
        return true;
    }
}

Intersection of Two Arrays

Given two integer arrays nums1 and nums2, return an array of their intersection. Each element in the result must be unique and you may return the result in any order.

Example:

Input: nums1 = [1,2,2,1], nums2 = [2,2]
Output: [2]

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int i : nums1) {
            if (map.containsKey(i)){
                map.put(i,map.get(i)+1);
            }else {
                map.put(i,1);
            }
        }
      //Note: Here can't use ArrayList since we need no repeatable result.
        HashSet<Integer> integers = new HashSet<>();
        for (int i : nums2) {
            if (map.containsKey(i)){
                integers.add(i);
            }
        }
        return integers.stream().mapToInt(Integer::intValue).toArray();
    }
}

Happy Number

Write an algorithm to determine if a number n is happy.

A happy number is a number defined by the following process:

• Starting with any positive integer, replace the number by the sum of the squares of its digits.
• Repeat the process until the number equals 1 (where it will stay), or it loops endlessly in a cycle which does not include 1.
• Those numbers for which this process ends in 1 are happy.

Return true if n is a happy number, and false if not.

The problem states that there will be an infinite loop, which means that during the summation process, the sum will repeat.

When we need to quickly determine whether an element appears in a set, we should consider using a hash method.

Therefore, we use a hash method to determine if this sum has appeared before. If it repeats, we return false; Otherwise, we continue until the sum becomes

public class Solution202 {
    public boolean isHappy(int n) {
        if (n==1){
            return true;
        }
      //Use HashSet rather than ArrayList
        HashSet<Integer> set = new HashSet<>();
        while (true){
            int sum = getSum(n);
            if (sum==1){
                return true;
            }
            if (set.contains(sum)){
                return false;
            }
            set.add(sum);
            n = sum;
        }
    }
  //Calculate each loop's n
    public int getSum(int n){
        int sum = 0;
        while (n>0){
            int digit = n%10;
            sum += digit*digit;
            n = n/10;
        }
        return sum;
    }
}