Linked list advanced
- Linked list basic
- Linked list basic
- Linked list advancedYou are here
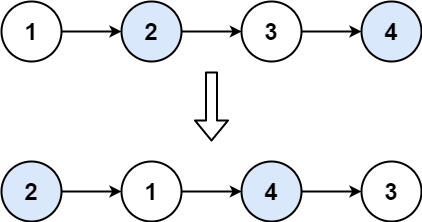
Swap Nodes in Pairs
Given a linked list, swap every two adjacent nodes and return its head. You must solve the problem without modifying the values in the list’s nodes (i.e., only nodes themselves may be changed.)
Use normal simulation:
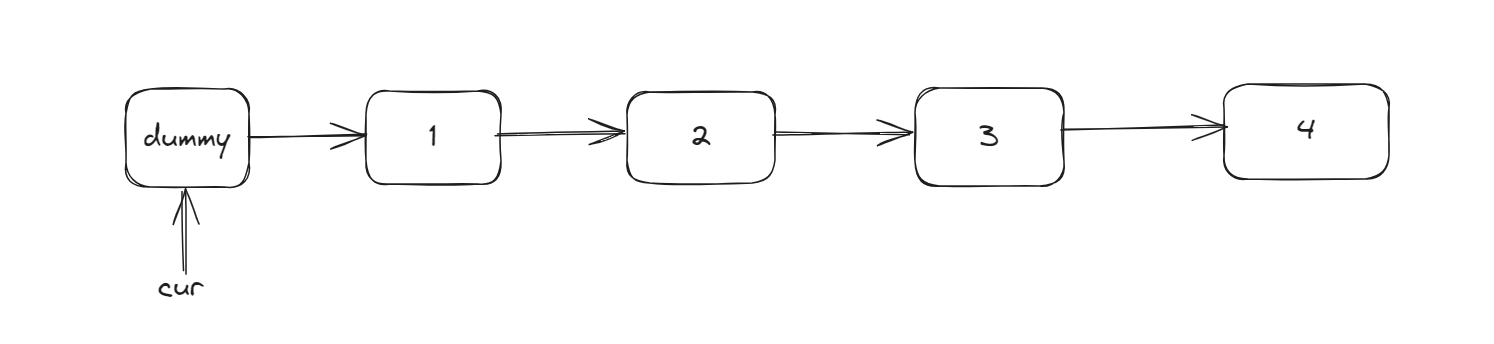
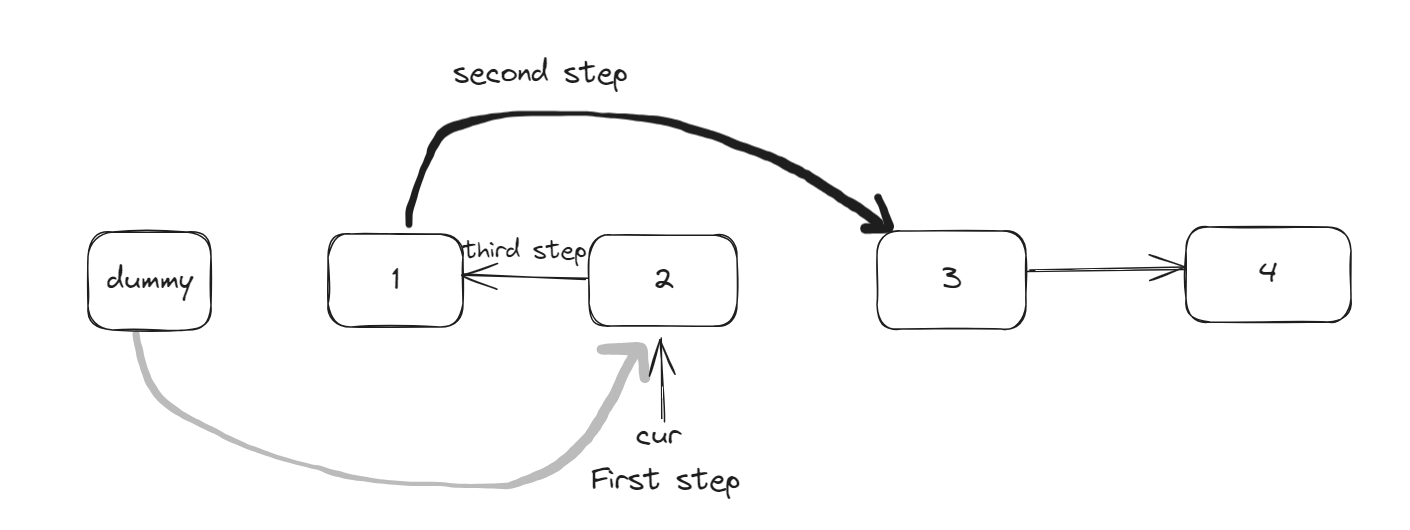
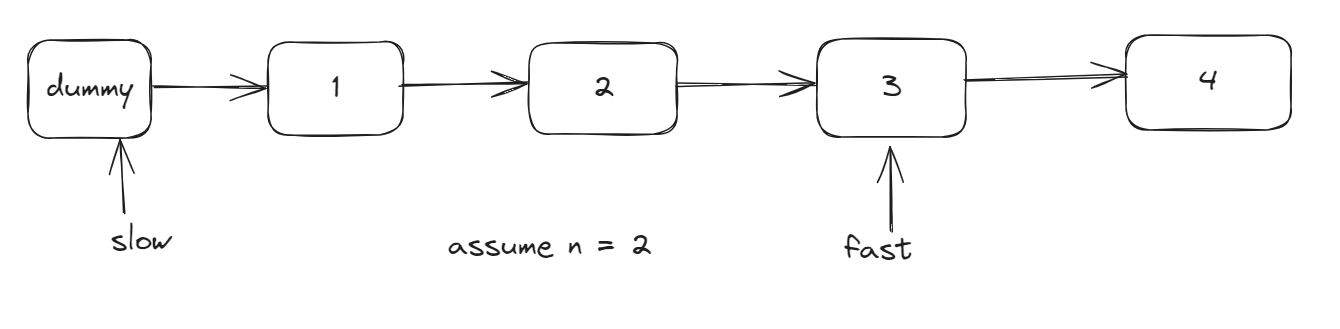
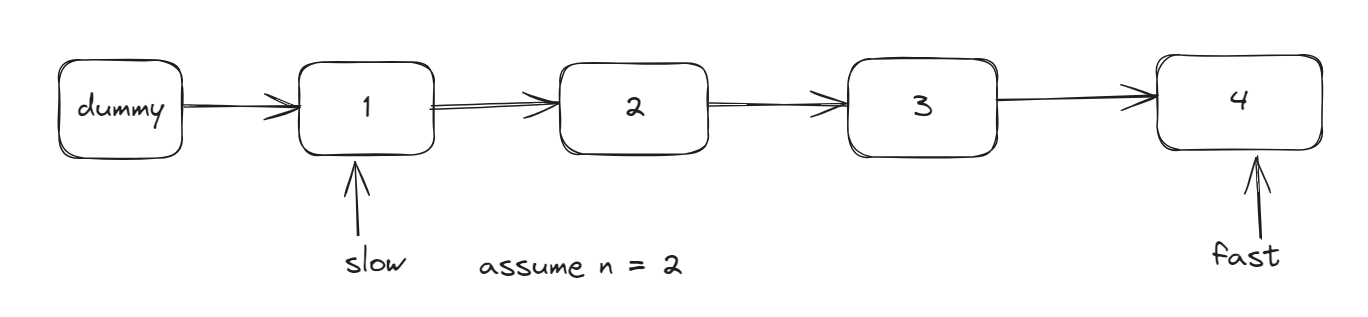
Initially, the temporary pointer ‘cur’ points to the dummy head node.
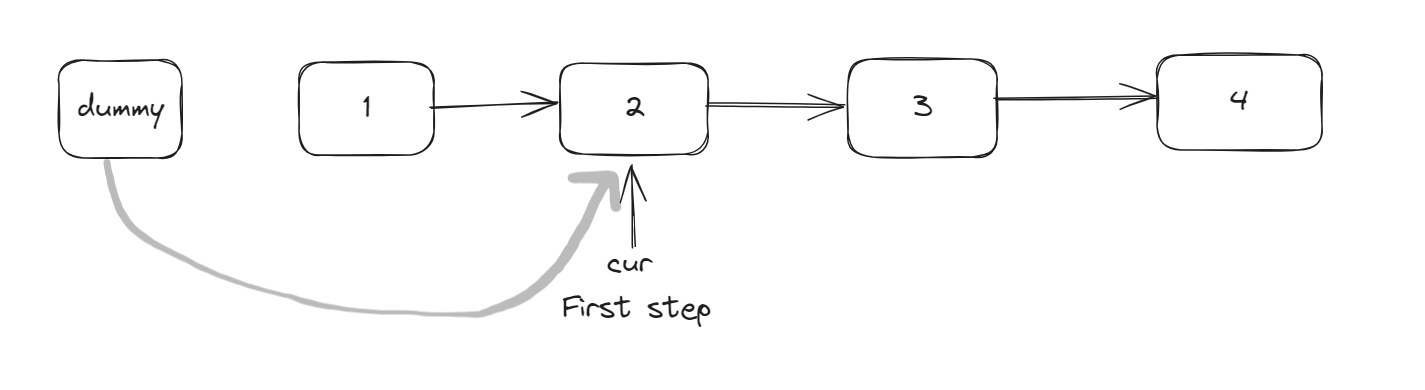
- The first step is to move the temporary pointer ‘cur’ to point to the second node.
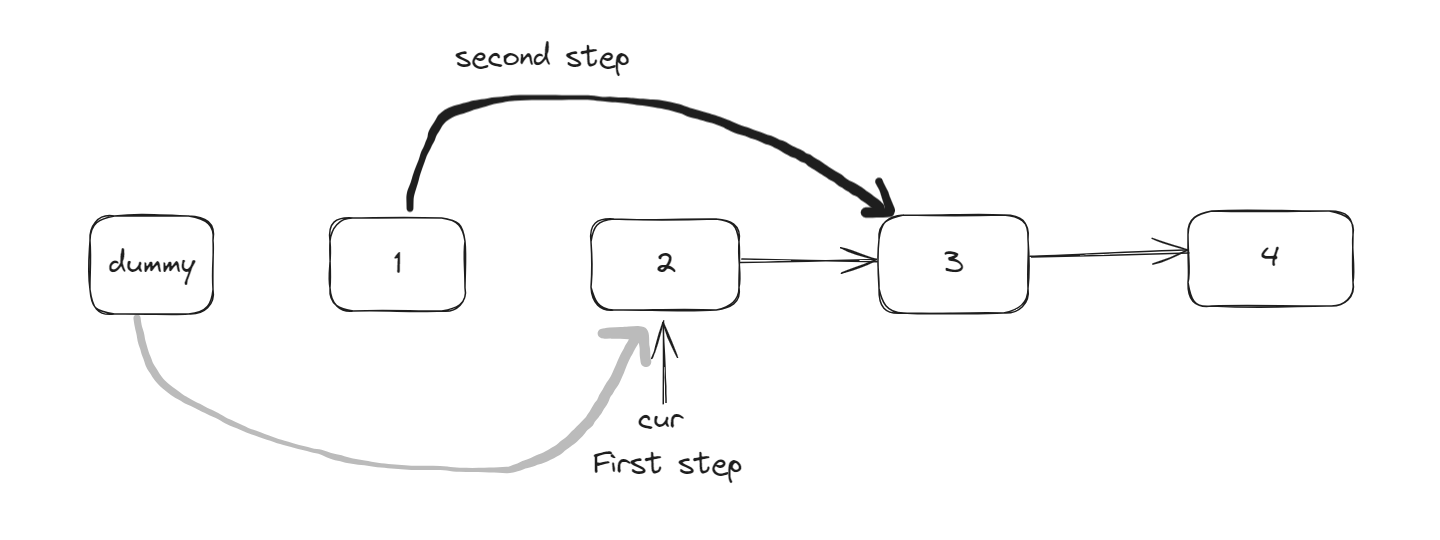
- The second step is making the ‘next’ pointer of the first node point to cur’s next(saved in the first step).
- The third step is to make the pointer of the second node point to the first node.
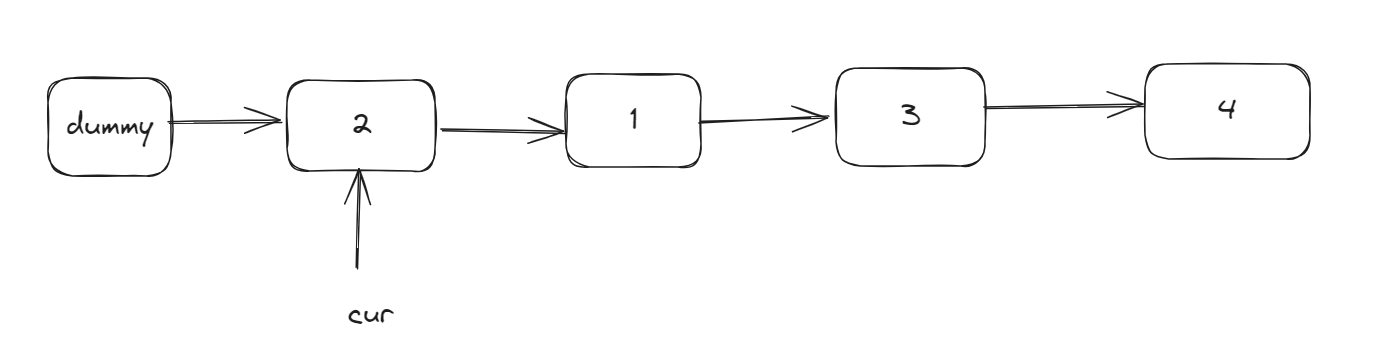
now we have this:
And if you need go to next loop, just set cur = cur.next.next;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public ListNode swapPairs(ListNode head) {
ListNode dummy = new ListNode(0,head);//dummy head node
ListNode cur = dummy;//Initial the cur point to the dummy head node
while(cur.next != null && cur.next.next != null){
ListNode first = cur.next;//first node
ListNode second = cur.next.next;//second node
//Three steps to go
//first step
cur.next = second;
//second step
first.next = second.next;
//third step
second.next = first;
//handle the next loop
cur = cur.next.next;
}
return dummy.next;
}
}
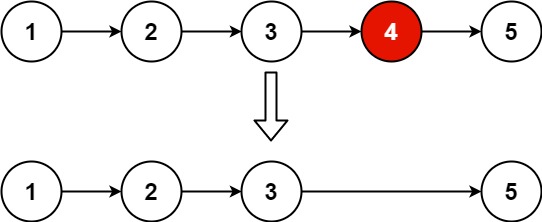
Remove Nth Node From End of List
Given the
headof a linked list, remove thenthnode from the end of the list and return its head.Example Input & Output:
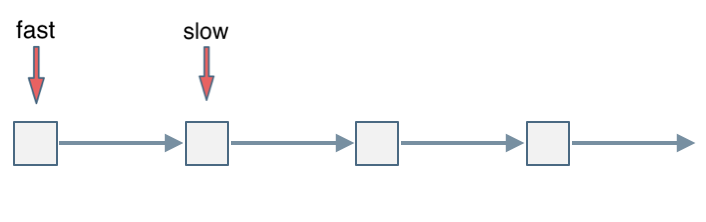
Typical fast and slow pointer problem.
Define two pointers. Let fast move n+1 steps first, then have fast and slow move synchronously until fast reaches Null. At this point, slow’s next is the element to be deleted, then delete it.”
We can go through the following steps to solve this question:
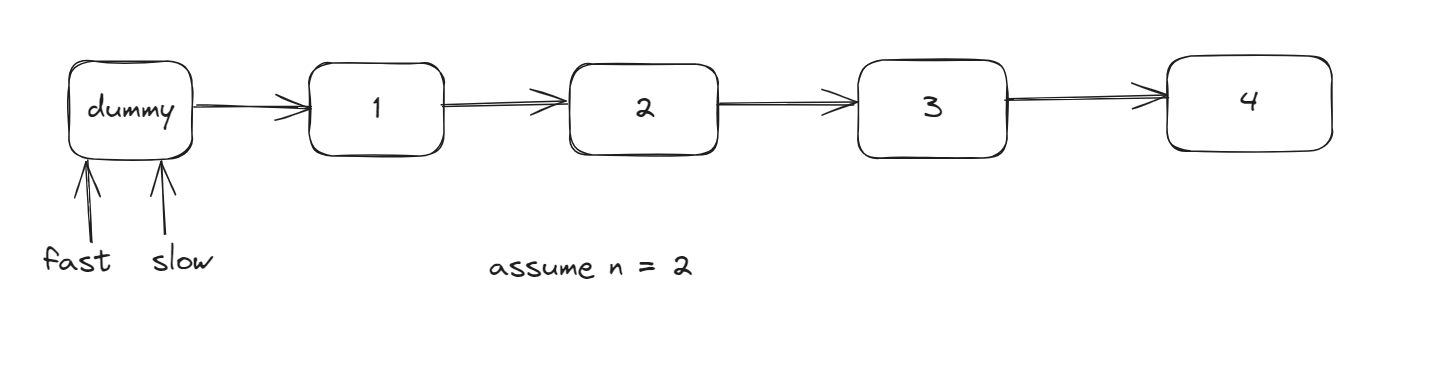
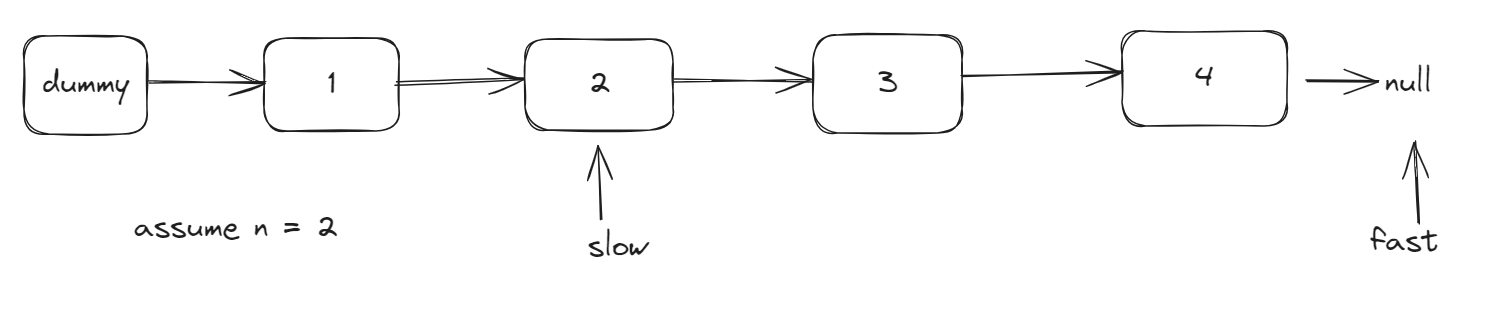
- Define fast and slow pointers, with initial values set for the dummy head node.
- The fast pointer first moves
n+1steps. Why not n? Since only this way, when moving simultaneously, the slow pointer can point to the node just before the one that needs to be deleted(or simply remember to move the fast point to the one that needs to be deleted).
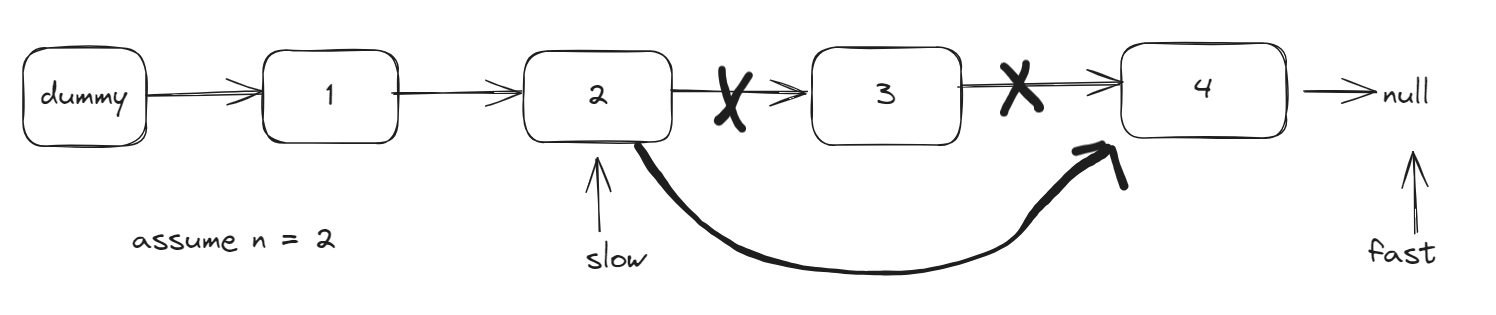
- Fast and slow pointers move simultaneously until the fast pointer points to the end.
- Finally, delete the node next to the one pointed to by the slow pointer.
Here is the code:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode dummy = new ListNode(0,head);
ListNode fast = dummy;
ListNode slow = dummy;
//move fast pointer n+1 steps
for(int i=0;i<=n;i++){
fast = fast.next;
}
//fast and slow pointers move simultaneously
while(fast!=null){
fast = fast.next;
slow = slow.next;
}
slow.next = slow.next.next;
return dummy.next;
}
}
Intersection of Two Linked Lists
Given the heads of two singly linked-lists
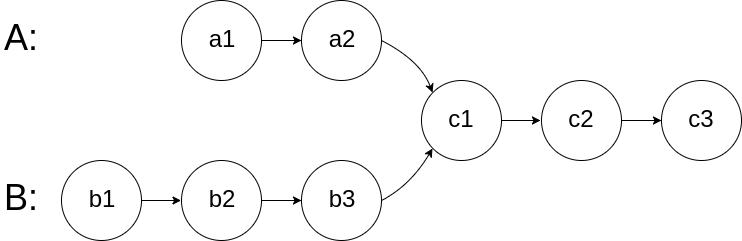
headAandheadB, return the node at which the two lists intersect. If the two linked lists have no intersection at all, returnnull.For example, the following two linked lists begin to intersect at node
c1:The test cases are generated such that there are no cycles anywhere in the entire linked structure.
Note that the linked lists must retain their original structure after the function returns.
skipA- The number of nodes to skip ahead inlistA(starting from the head) to get to the intersected node.skipB- The number of nodes to skip ahead inlistB(starting from the head) to get to the intersected node.Example:
Method one:
In simple terms, it’s about finding the pointer to the intersection node of two linked lists. Be note that the intersection is not about equal values, but about equal pointers.
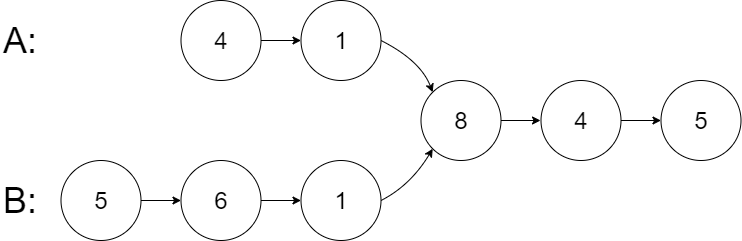
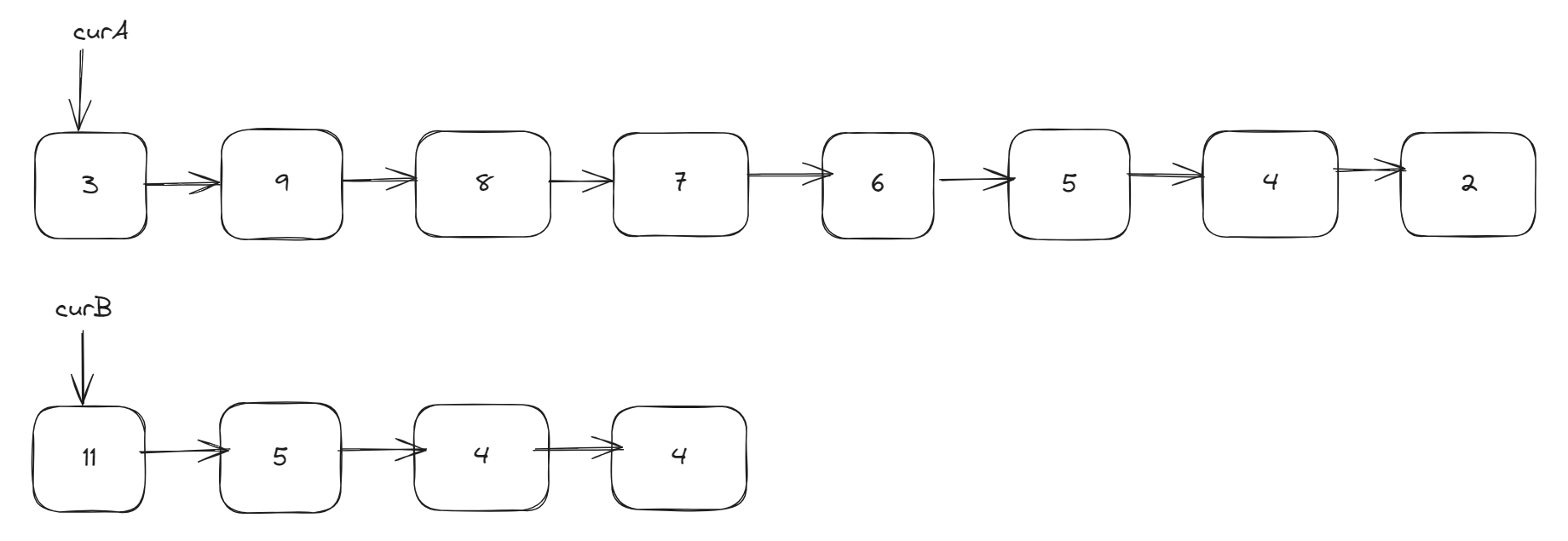
Assume we have two linked list as following, pointer curA point to A’s head node, curB point to B’s head node.
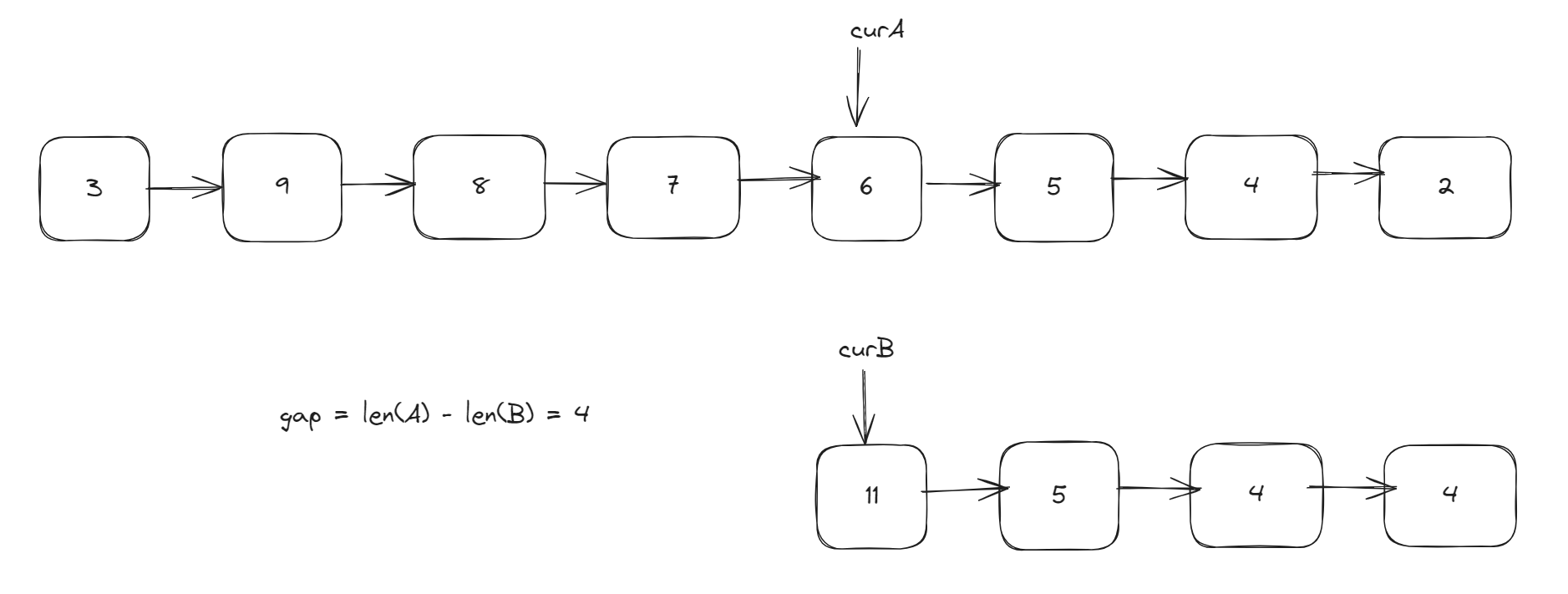
We calculate the lengths of the two linked lists and find the difference between these lengths. Then we move curA to the position where it aligns with the end of curB, as shown in the following fiture:
At this point, we can compare whether curA and curB are the same. If they are not the same, move curA and curB backward simultaneously. Is curA==curB is encountered, the intersection is found.
Otherwise, exit the loop and return a null pointer.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode curA = headA;
ListNode curB = headB;
int lenA = 0, lenB = 0;
while(curA != null){
curA = curA.next;
lenA++;
}
while(curB != null){
curB = curB.next;
lenB++;
}
curA = headA;
curB = headB;
//let curA and lenA is the longer or greater
if (lenB > lenA){
//swap curA and curB
ListNode temp = curA;
curA = curB;
curB = temp;
//swap lenA and lenB
int tmpLen = lenA;
lenA = lenB;
lenB = tmpLen;
}
//figure the diff between lenA and lenB
int gap = lenA - lenB;
//let curA and curB in the same position
while(gap-- > 0){
curA = curA.next;
}
//traver curA and curB, if equals, return
while(curA != null){
if(curA == curB){
return curA;
}
curA = curA.next;
curB = curB.next;
}
return null;
}
}
Method two:
We can use two iterations to do that. In the first iteration, we will reset the pointer of one linkedlist to the head of another linkedlist after it reaches the tail node. In the second iteration, we will move two pointers until they points to the same node. Our operations in first iteration will help us counteract the difference. So if two linkedlist intersects, the meeting point in second iteration must be the intersection point. If the two linked lists have no intersection at all, then the meeting pointer in second iteration must be the tail node of both lists, which is null.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if(headA == null || headB == null) return null;
ListNode a = headA;
ListNode b = headB;
while(a != b){
a = a == null? headB : a.next;
b = b == null? headA : b.next;
}
return a;
}
}
Visualization of this solution: Case 1 (Have Intersection & Same Len):
1
2
3
4
5
6
7
a
A: a1 → a2 → a3
↘
c1 → c2 → c3 → null
↗
B: b1 → b2 → b3
b
1
2
3
4
5
6
7
a
A: a1 → a2 → a3
↘
c1 → c2 → c3 → null
↗
B: b1 → b2 → b3
b
1
2
3
4
5
6
7
a
A: a1 → a2 → a3
↘
c1 → c2 → c3 → null
↗
B: b1 → b2 → b3
b
1
2
3
4
5
A: a1 → a2 → a3
↘ a
c1 → c2 → c3 → null
↗ b
B: b1 → b2 → b3
Since a == b is true, end loop while(a != b), return the intersection node a = c1.
Case 2 (Have Intersection & Different Len):
1
2
3
4
5
6
7
a
A: a1 → a2
↘
c1 → c2 → c3 → null
↗
B: b1 → b2 → b3
b
1
2
3
4
5
6
7
a
A: a1 → a2
↘
c1 → c2 → c3 → null
↗
B: b1 → b2 → b3
b
1
2
3
4
5
6
A: a1 → a2
↘ a
c1 → c2 → c3 → null
↗
B: b1 → b2 → b3
b
1
2
3
4
5
A: a1 → a2
↘ a
c1 → c2 → c3 → null
↗ b
B: b1 → b2 → b3
1
2
3
4
5
A: a1 → a2
↘ a
c1 → c2 → c3 → null
↗ b
B: b1 → b2 → b3
1
2
3
4
5
A: a1 → a2
↘ a = null, then a = b1
c1 → c2 → c3 → null
↗ b
B: b1 → b2 → b3
1
2
3
4
5
6
A: a1 → a2
↘
c1 → c2 → c3 → null
↗ b = null, then b = a1
B: b1 → b2 → b3
a
1
2
3
4
5
6
7
b
A: a1 → a2
↘
c1 → c2 → c3 → null
↗
B: b1 → b2 → b3
a
1
2
3
4
5
6
7
b
A: a1 → a2
↘
c1 → c2 → c3 → null
↗
B: b1 → b2 → b3
a
1
2
3
4
5
A: a1 → a2
↘ b
c1 → c2 → c3 → null
↗ a
B: b1 → b2 → b3
Since a == b is true, end loop while(a != b), return the intersection node a = c1.
Case 3 (Have No Intersection & Same Len):
1
2
3
4
a
A: a1 → a2 → a3 → null
B: b1 → b2 → b3 → null
b
1
2
3
4
a
A: a1 → a2 → a3 → null
B: b1 → b2 → b3 → null
b
1
2
3
4
a
A: a1 → a2 → a3 → null
B: b1 → b2 → b3 → null
b
1
2
3
4
a = null
A: a1 → a2 → a3 → null
B: b1 → b2 → b3 → null
b = null
Since a == b is true (both refer to null), end loop while(a != b), return a = null.
Case 4 (Have No Intersection & Different Len):
1
2
3
4
a
A: a1 → a2 → a3 → a4 → null
B: b1 → b2 → b3 → null
b
1
2
3
4
a
A: a1 → a2 → a3 → a4 → null
B: b1 → b2 → b3 → null
b
1
2
3
4
a
A: a1 → a2 → a3 → a4 → null
B: b1 → b2 → b3 → null
b
1
2
3
4
a
A: a1 → a2 → a3 → a4 → null
B: b1 → b2 → b3 → null
b = null, then b = a1
1
2
3
b a = null, then a = b1
A: a1 → a2 → a3 → a4 → null
B: b1 → b2 → b3 → null
1
2
3
4
b
A: a1 → a2 → a3 → a4 → null
B: b1 → b2 → b3 → null
a
1
2
3
4
b
A: a1 → a2 → a3 → a4 → null
B: b1 → b2 → b3 → null
a
1
2
3
4
b
A: a1 → a2 → a3 → a4 → null
B: b1 → b2 → b3 → null
a
1
2
3
4
b = null
A: a1 → a2 → a3 → a4 → null
B: b1 → b2 → b3 → null
a = null
Since a == b is true (both refer to null), end loop while(a != b), return a = null.
Notice that if list A and list B have the same length, this solution will terminate in no more than 1 traversal; if both lists have different lengths, this solution will terminate in no more than 2 traversals – in the second traversal, swapping a and b synchronizes a and b before the end of the second traversal. By synchronizing a and b I mean both have the same remaining steps in the second traversal so that it’s guaranteed for them to reach the first intersection node, or reach null at the same time (technically speaking, in the same iteration) – see Case 2 (Have Intersection & Different Len) and Case 4 (Have No Intersection & Different Len).
Linked List Cycle II
Given the
headof a linked list, return the node where the cycle begins. If there is no cycle, returnnull.There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the
nextpointer. Internally,posis used to denote the index of the node that tail’snextpointer is connected to (0-indexed). It is-1if there is no cycle. Note thatposis not passed as a parameter.Do not modify the linked list.
Example:
The main points being examined are:
- Determining whether a linked list has a cycle.
We can use the fast and slow pointer method.
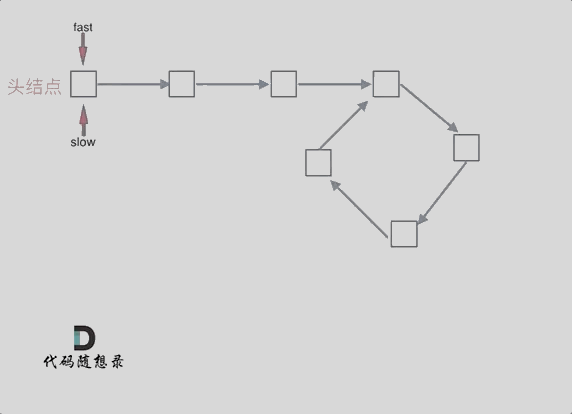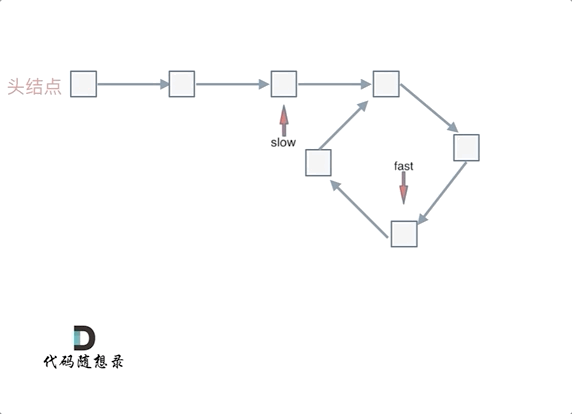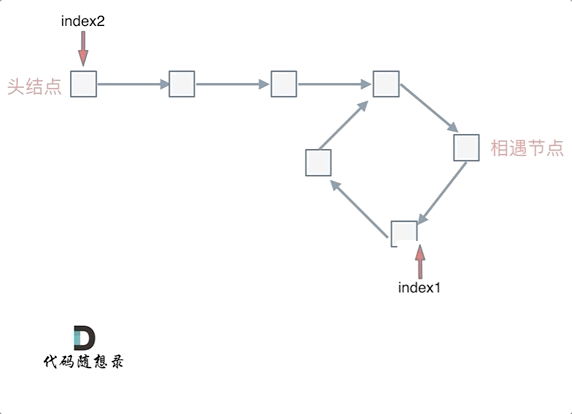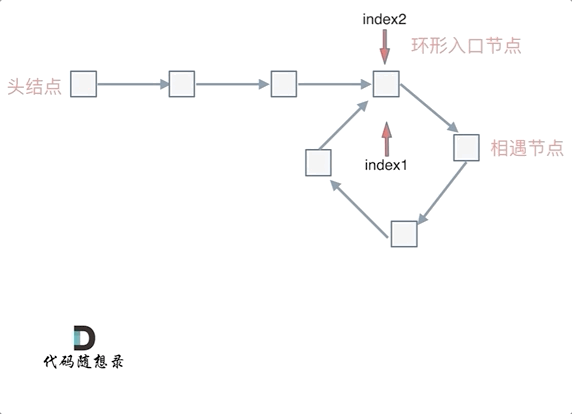
Define two pointers, ‘fast’ and ‘slow’, starting from the head node. The fast pointer moves two nodes at a time, while the slow pointer moves one node at a time. If the fast and slow pointers meet during this process, it indicates that the linked list has a cycle.
Why is it that if the fast pointer moves two nodes at a time and the slow pointer moves one node at a time, they will definitely meet within the cycle if there is one, rather always missing each other?
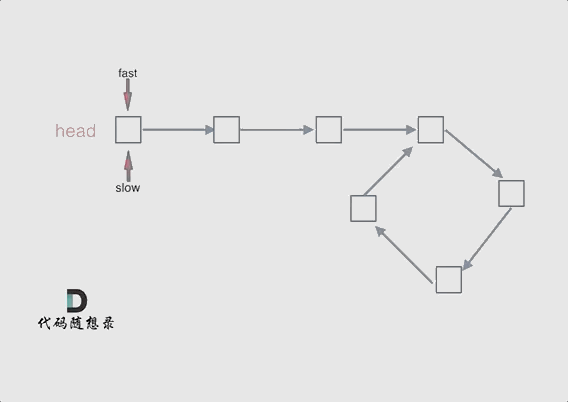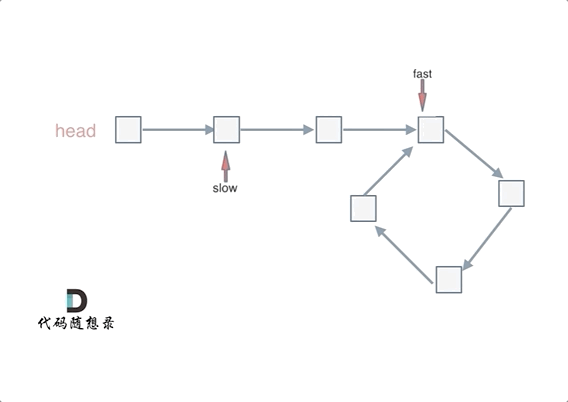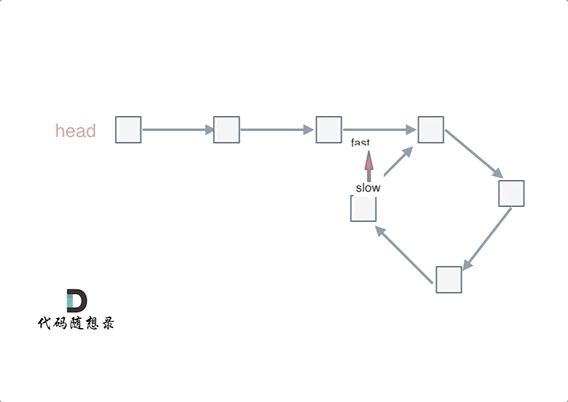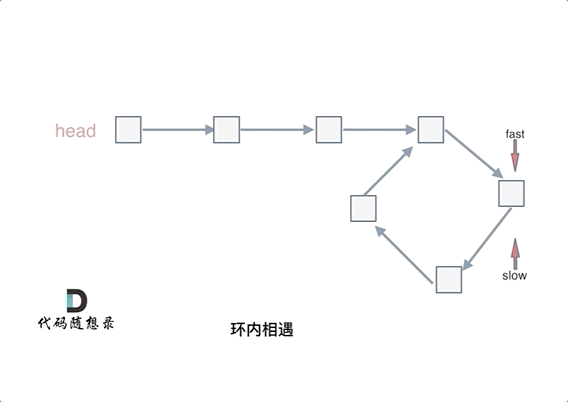
We can draw cycle, and then let the fast pointer start chasing the slow pointer from any node.
The fast and slow pointers each take one more step, and then fast and slow meet. This is because fast moves two steps while slow moves one step. In relation to slow, fast is actually approaching slow one node at a time, so fast will definitely overlap with slow.
- If there is a cycle, how to find the entrance of this cycle.
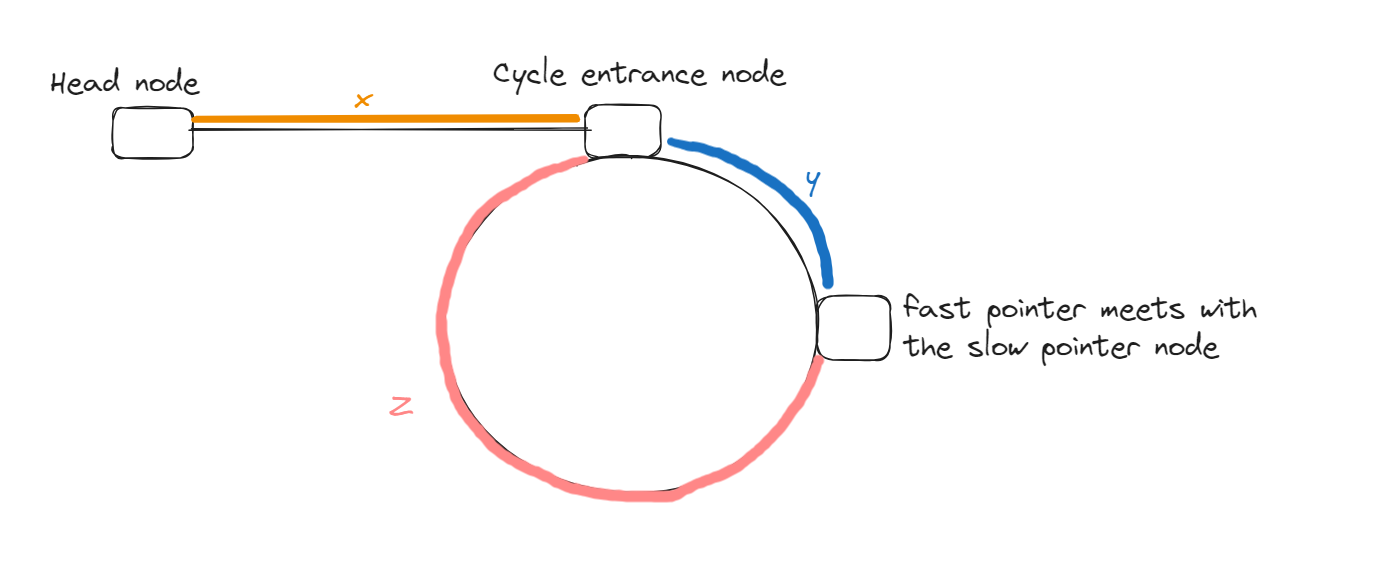
Suppose the number of nodes from the head node to the cycle entrance node is x.
The number of nodes from the cycle entrance node to the node where the fast pointer meets the slow pointer is y.
The number of nodes from the meeting point back to the cycle entrance node is z.
Then, at the point of meeting: The number of nodes the slow pointer has traversed is: x+y.
The number of nodes the fast pointer has traversed is: x+y+n(y+z), where n is the number of complete cycles the fast pointer has made in the ring before meeting the slow pointer, and (y+z) is the number of nodes in one complete cycle.
Since the fast pointer moves two nodes in one step, while the slow pointer moves one node in one step, the number of nodes traversed by the fast pointer = the number of nodes traversed by the slow pointer * 2.
` (x+y) * 2 = x + y + n (y+z)`
-> x + y = n (y + z)
We need to find the entrance node - regard as x
-> x = n (y + z) - y = (n-1) (y+z) + z , here n >1
What this formula mean?
Let’s first take the case where n is 1 as an example, meaning that the fast pointer meets the slow pointer after making one complete cycle in the ring.
When n is 1, the formula simplifies to x = z.
This means that if we start one pointer from the head node and another pointer from the meeting point, and these two pointers each move one node at a time, then the node where these two pointers meet is the entrance node of the cycle.
So what if n is greater than 1?
Actually, this situation is the same as when n is 1. The only different is that the fast pointers make n-1 additional cycles in the ring before meeting the slow pointer. The meeting point is still the entrance node of the cycle.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode fast = head;
ListNode slow = head;
while(fast != null && fast.next != null){
fast = fast.next.next;
slow = slow.next;
//When the fast and slow pointers meet, at this point, start searching simultaneously from the head and the meeting point until they meet.
if(fast == slow){
ListNode head1 = head;
ListNode head2 = fast;
while(head != fast){
head = head.next;
fast = fast.next;
}
return fast;
}
}
return null;
}
}
Why at the first meeting point in the cycle, slow’s passed nodes is x+y , rather than ` x + some number of cycle lengths + y`?
First, when slow enters the cycle, fast must have already entered the cycle.
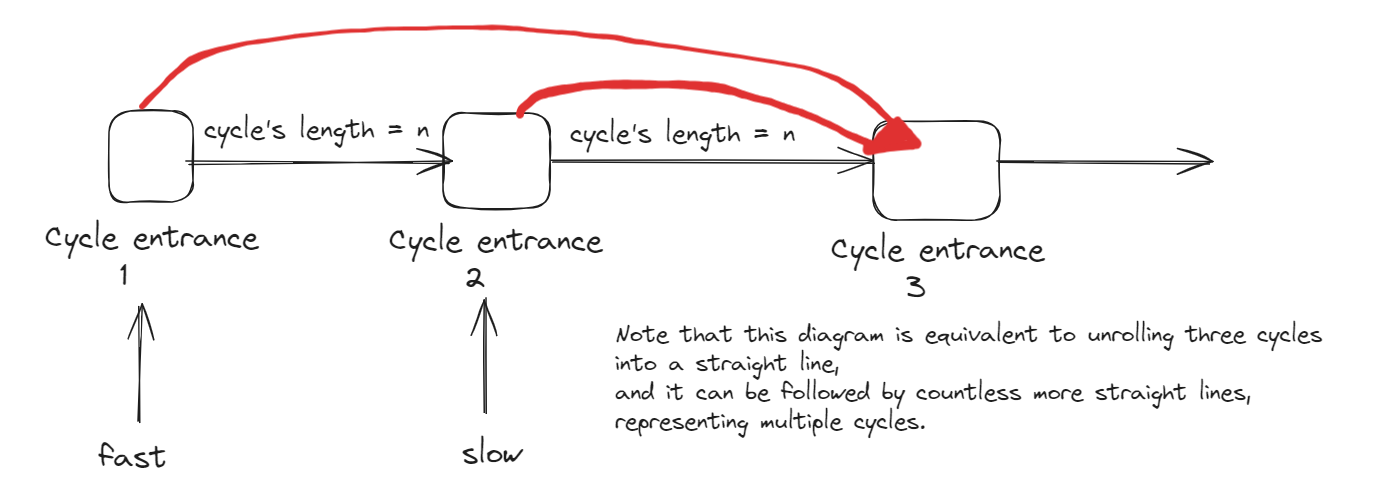
If slow enters the cycle entrance and fast is also at the cycle entrance, then if we unroll this cycle into a straight line, it would look like the following diagram:
It can be seen that if slow and fast start walking from the cycle entrance at the same time, they will definitely meet at the third cycle entrance. Slow will have walk ed on cycle, and fast will have walked two cycles.
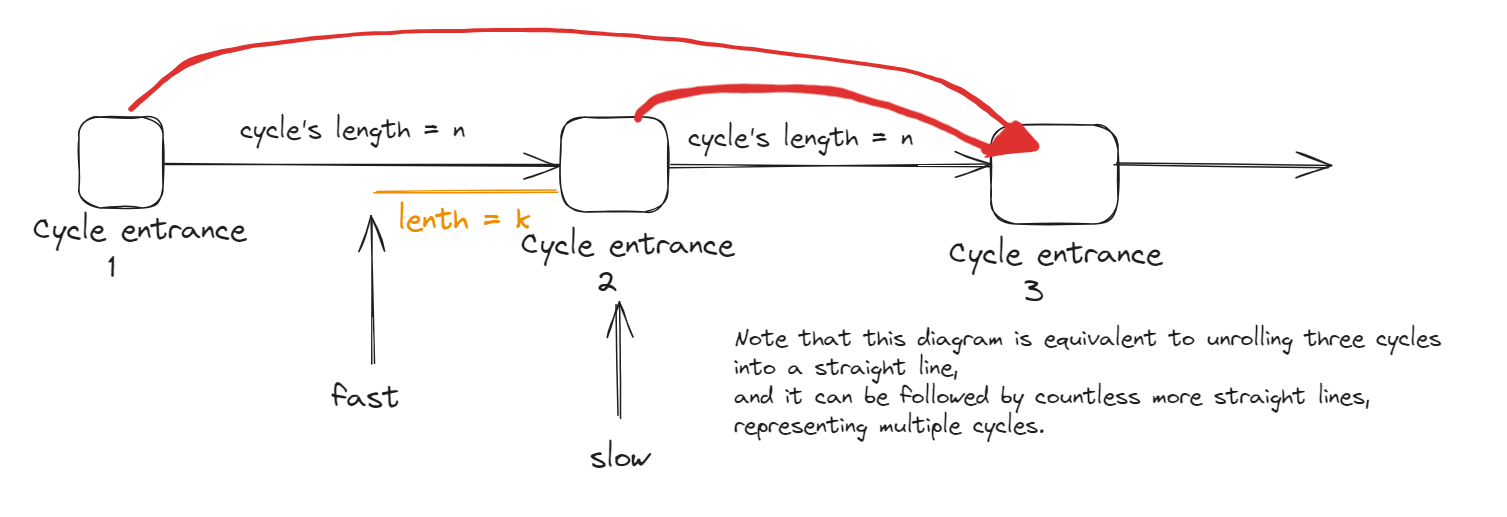
The key point is that when slow enters the cycle, fast must be at some position within the cycle, as shown in the diagram:
When fast pointer walked at the cycle entrance 3, it already passed k + n nodes, slow correspondonly pass (k + n) / 2 nodes.
Since k < n (see above image)
-> (k + n) / 2 < n
This means the slow pointer must not walked at cycle entrance 3, meanwhile the fast pointer already at cycle entrance 3.
What this mean?
This means **they have already met in the cycle where the slow points starts walking **
Why can’t fast jump over slow?
Mentioned above, the fast pointer moves one node at a time relative to slow, so it’s impossible for it to jump over.